|
Maple is a
computer algebra system that saves its users time and
routine work. In this course we are using Maple version 7
as a tool with complex numbers to first facilitate
understanding and secondly to help us do the work that a
machine can do faster thus leaving us with more time to
think. Maple commands are preceded by > and always end
with ;
To invoke a help session about complex
numbers in Maple use:
>?complex
1.
Activity 1 – Getting familiar with Maple with some
examples on complex numbers
Examples:
Find the modulus (absolute!) value
of a complex number:
>
abs(2+19*I);

The
nice thing about Maple is that it can do symbolic
representation as well as calculation:
>
a:=abs(2*z+3);

> z:=1+I;

> a;
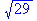
2.
Activity 2 Maple
explorations on your own
Maple contains many packages. To load
up the Linear Algebra package , for example, use:
>with(LinearAlgebra):
Note the colon : is used instead of the
semicolon; because the latter will list all the functions
in Linear Algebra.
Now play around with some examples of
your own. |

